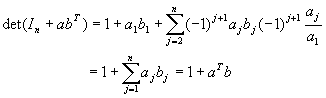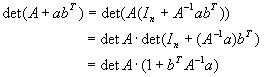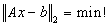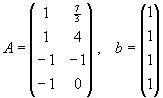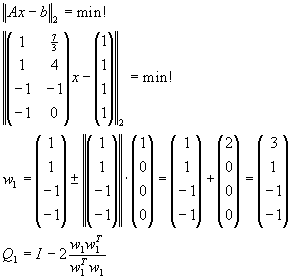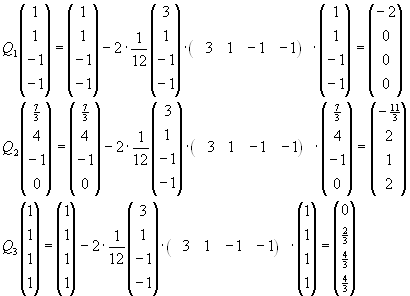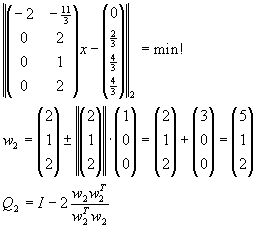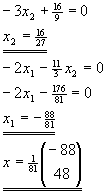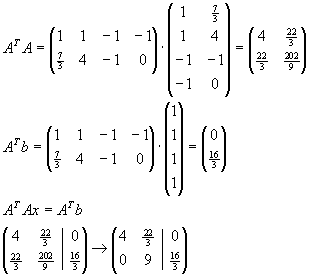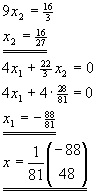Verschiedene Aufgaben
Aufgabe 1
Geben Sie die Wahrheitswertetafeln folgender Aussagen an:
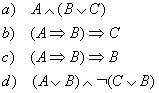
Können Sie c) und d) vereinfachen?
Lösung für Aufgabe 1
| a) |
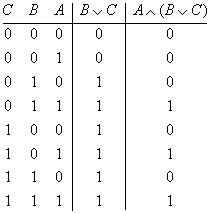 |
| b) |
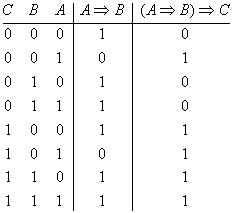 |
| c) |
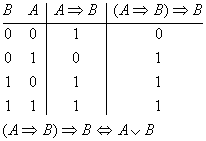 |
| d) |
 |
Aufgabe 2
Beweisen Sie mittels vollständiger Induktion
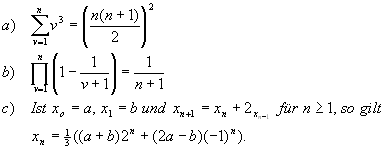
Lösung für Aufgabe 2
| a) |
vollständige Induktion
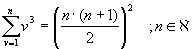
Induktionsanfang:
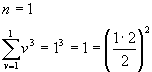
Induktionsschritt:
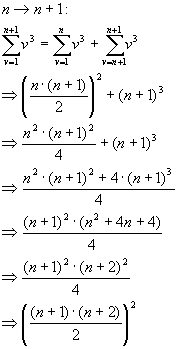
|
| b) |
vollständige Induktion
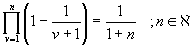
Induktionsanfang:
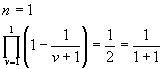
Induktionsschritt:
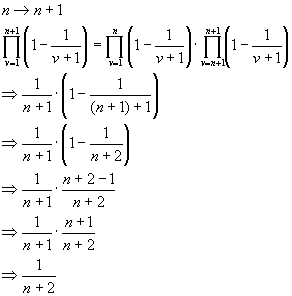
|
| c) |
vollständige Induktion
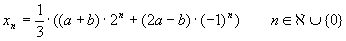
Induktionsanfang:
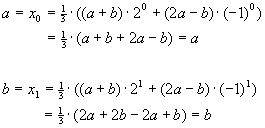
Induktionsschritt:
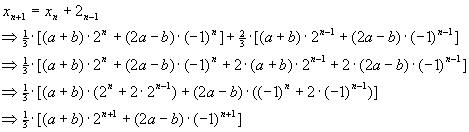
|
Aufgabe 3
| a) |
Man untersuche die folgenden Vektoren jeweils auf ihre lineare Abhängigkeit und bestimme jeweils eine Basis
und die Dimension des von ihnen aufgespannten Unterraums
|
Lösung für Aufgabe 3
| a) |
| (i) |
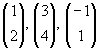 |
sind linear abhängig, denn die maximale Anzahl linear unabhängiger Vektoren im |
 |
ist 2. |
| Die Vektoren |
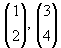 |
sind linear unabhängig und bilden die Basis |
|
W = span |
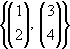 |
|
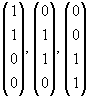
| (ii) |
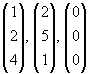 |
sind linear abhängig, denn |
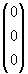 |
ist der Nullvektor. |
| Die Vektoren |
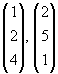 |
sind linear unabhängig und bilden die Basis |
|
W = span |
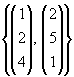 |
|
| (iii) |
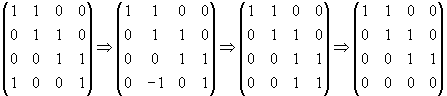 |
| Die Vektoren sind linear abhängig. |
| Die Vektoren |
 |
sind linear unabhängig und bilden die Basis |
|
W = span |
 |
|
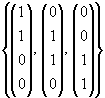
| (iv) |
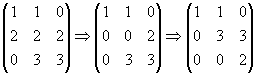 |
| Die Vektoren sind linear unabhängig. |
| Die Vektoren |
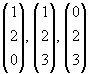 |
bilden die Basis |
|
W = span |
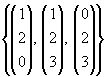 |
|
|
| b) |
| linear abhängig für |
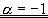 |
. |
|
Aufgabe 4
Gegeben seien die Matrizen
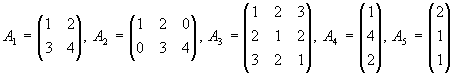 .
.
| a) |
Bestimmen Sie alle Produkte von je 2 dieser Matrizen, die definiert sind.
|
| b) |
Bestimmen Sie alle Produkte der Form
|
| 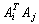 |
und |
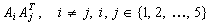 |
soweit sie definiert sind.
|
Lösung für Aufgabe 4
Aufgabe 5
| Bestimmen Sie die Parameter |
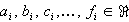 |
, so daß die Matrix |
|
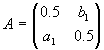 |
orthogonal und |
|
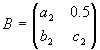 |
orthogonal und symmetrisch ist. |
|
und die komplexen Matrizen |
|
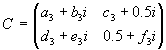 |
und |
|
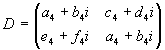 |
|
unitär und hermitisch sind. |
Lösung für Aufgabe 5
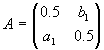
A·AT=I2
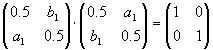
0.5·a1+0.5·b1=0
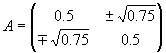
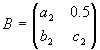
B·BT=I2
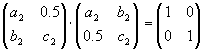
a2·b2+0.5·c2=0
b22+c22=1
B=BT
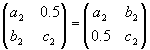
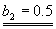
b22+c22=1
(0.5)2+c22=1
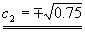
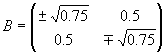
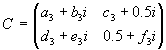
C=C*
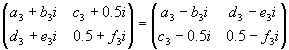
| a3+b3i=a3-b3i |
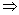 |
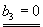
|
| c3+0.5i=d3-e3i |
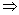 |
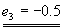
|
d3+e3i=c3-0.5i
| 0.5+f3i=0.5-f3i |
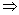 |
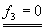
|
c3=d3
C·C*=I2
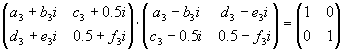
|
a32+b32+c32-0.25i2=1
|
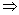 |
a32+c32=0.75 |
d32+e32+0.25+f32=1
d32+0.5=1
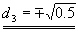
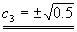
a32+0.5=0.75
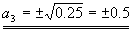
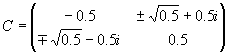
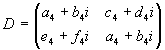
D=D*
| a4+b4i=a4-b4i |
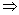 |
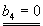 |
| c4+d4i=e4-f4i |
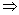 |
d4=-f4 |
e4+f4i=c4-d4i
a4+b4i=a4-b4i
e4=c4
D·D*=I2
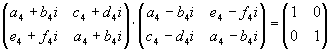
a42+b42+c42+d42=1
(e4+f4i)·a4+a4·(c4-d4i)=0
a4·e4+a4·f4+a4·c4-a4·d4i=0
a·(e4+f4i+c4-d4i)=0
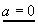
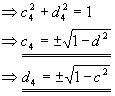
Es gibt 2 Lösungen:
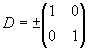
oder
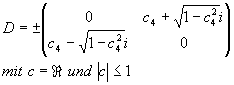
Aufgabe 6
| a) |
Man bestimme die Lösung X der Matrizengleichung A X + X AT = I2, wobei
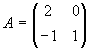 |
. |
|
| b) |
Man bestimme sämtliche Lösungen X der Matrizengleichung
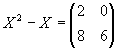
|
| c) |
Es sei a ein n-dimensionaler Spaltenvektor mit 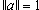 . Daraus werde die
(n, n)-Mtrix A = In - 2 a aT (A ist eine sog.
Householder-Matrix) gebildet. Man berechne A2. Was folgt hieraus für A-1
und allgemein für AP (p ganz)? . Daraus werde die
(n, n)-Mtrix A = In - 2 a aT (A ist eine sog.
Householder-Matrix) gebildet. Man berechne A2. Was folgt hieraus für A-1
und allgemein für AP (p ganz)?
|
Lösung für Aufgabe 6
| a) |
A·X+X·AT=I2
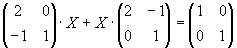
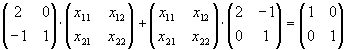
| -x11+x21+2·x21=0 |
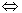 |
-x11+3·x21=0 |
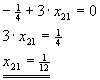
| 2·x12+x12-x11=0 |
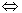 |
3·x12-x11=0 |
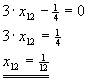
| -x12+x22-x21+x22=1 |
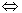 |
-x12+2·x22-x21=1 |
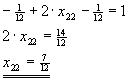
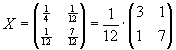
|
| b) |
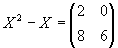
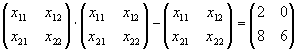
x21·x11+x22·x21-x21=8
x21·(x11+x22-1)=8
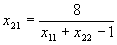
x11·x12+x21·xx22-x12=0
x12·(x11+x22-1)=0
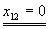
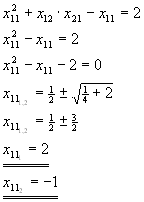
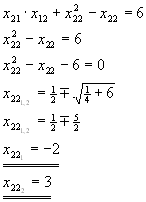
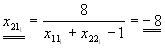
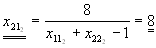
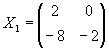
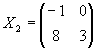
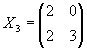
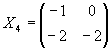
|
| c) |
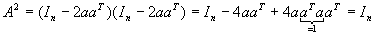
für gerade P ist AP=In
für ungerade P ist AP=A
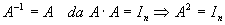
|
Aufgabe 7
| a) |
| Bestimmen Sie alle Lösungen für die folgenden Gleichungssysteme |
| (i) |
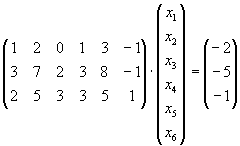 |
| (ii) |
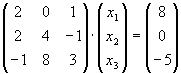 |
|
| b) |
| Diskutieren Sie die Lösungen des Gleichungssystems |
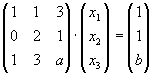 |
| in Abhängigkeit von den Parametern |
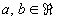 |
. |
|
|
Lösung für Aufgabe 7
| a) |
| (i) |
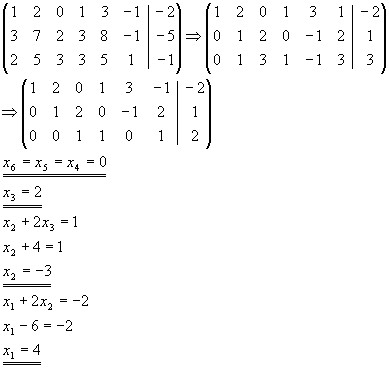
Berechnung der allgemeinen Lösung des homogenen Gleichungssystems
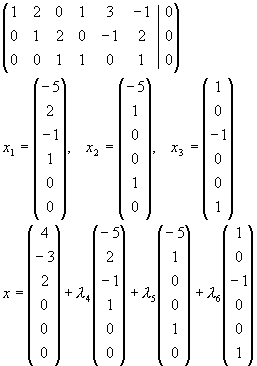
|
| (ii) |
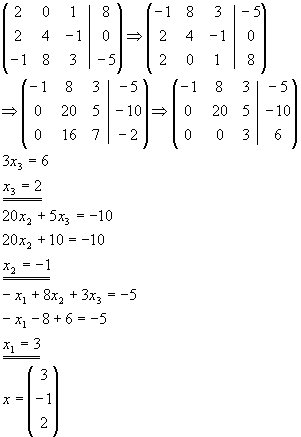 |
|
| b) |
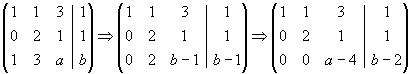
Das Gleichungssystem ist für a=4, b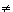 2 nicht lösbar. 2 nicht lösbar.
Für a=4, b=2 hat das Gleichungssystem unendlich viele Lösungen.
Eine Lösung ist z.B.:
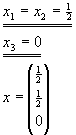
sonst ist die Lösung:
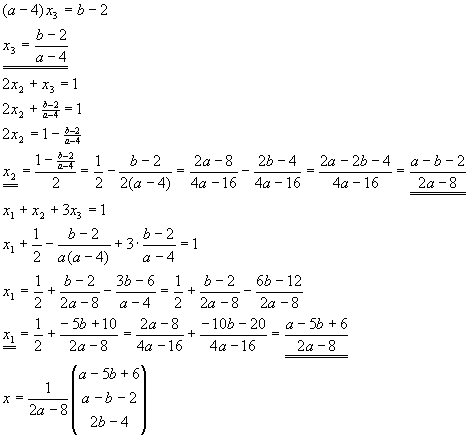
|
Aufgabe 8
Gegeben sei das lineare Gleichungssystem Ax=b mit
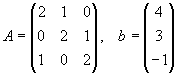
| a) |
Lösen Sie das lineare Gleichungssystem Ax=b nach dem Gaußschen Eliminationsverfahren. |
| b) |
Berechnen Sie mit dem Gauß-Jordan-Algorithmus die Inverse der Matrix A. |
| c) |
Bestimmen Sie die Lösungen des Gleichungssystems mit Hilfe der Inversen A-1 aus Teil b. |
Lösung für Aufgabe 8
| a) |
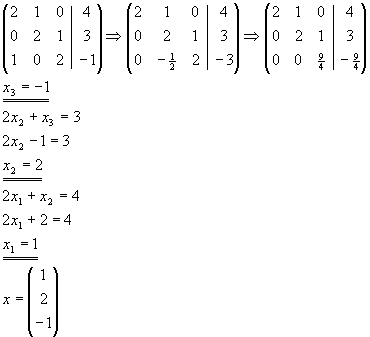 |
| b) |
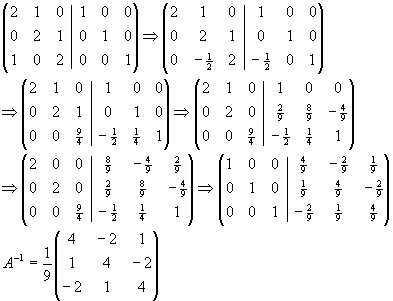 |
| c) |
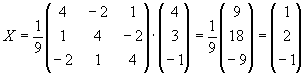 |
Aufgabe 9
| a) |
| Es seien |
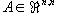 |
regulär und |
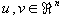 |
. |
| Man zeige, daß die Matrix B := A - uvT genau dann regulär ist, wenn |
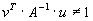 |
gilt, und daß dann |
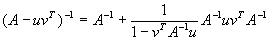 |
| gilt. |
|
| b) |
| Es sei |
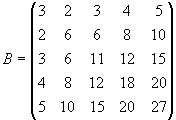 |
| Man löse das lineare Gleichungssystem |
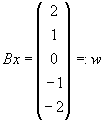 |
|
Lösung für Aufgabe 9
| b) |
Mit A=2In, u=(1 2 3 4 5)T und v=-u hat B die Darstellung B=A-vvT.
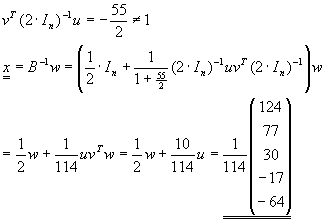
|
Aufgabe 10
Man stelle Gleichungen zur Bestimmung der Ströme im folgenden Netzwerk auf:
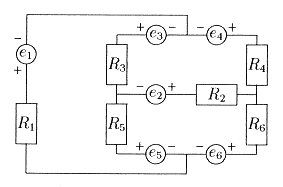
Man löse dieses Gleichungssystem für die folgenden Werte mittels Gauß-Elimination:
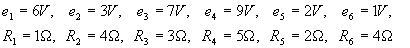
Lösung für Aufgabe 10
Nach dem Verfahren aus "Grundlagen der Elektrotechnik I" (Ameling) folgt:
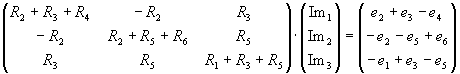
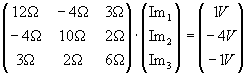
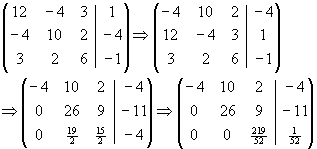
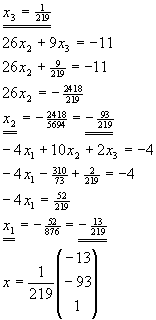
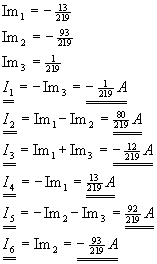
Aufgabe 11
Bestimmen Sie die LR-Zerlegung der Matrix
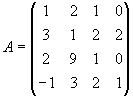
und lösen Sie die linearen Gleichungssysteme
| |
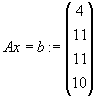 |
und |
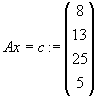 |
. |
Lösung für Aufgabe 11

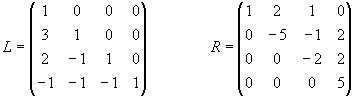
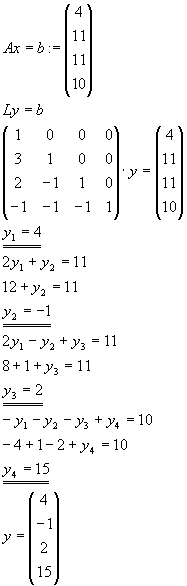
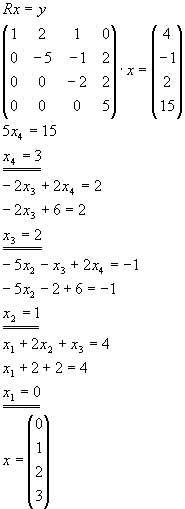
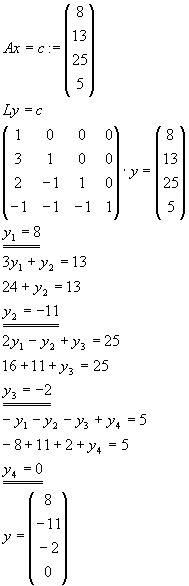
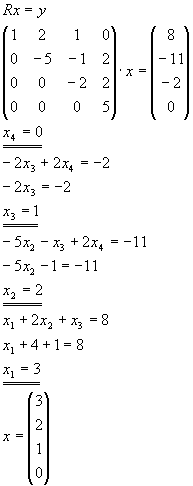
Aufgabe 12
Es sei
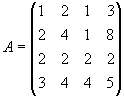
Bestimmen Sie für eine geeignete Permutationsmatrix P die LR-Zerlegung von PA und lösen
Sie hiermit das Gleichungssystem
| |
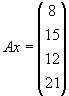 |
. |
Lösung für Aufgabe 12
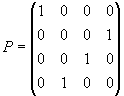
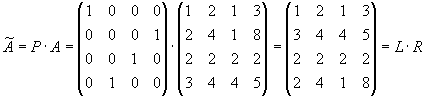
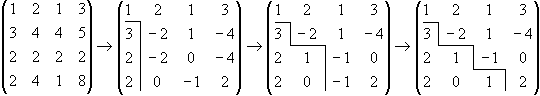
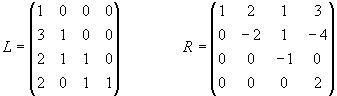
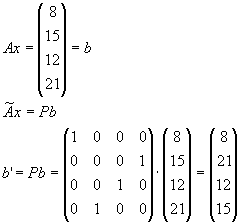
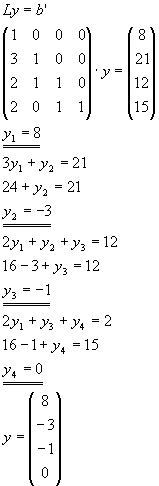
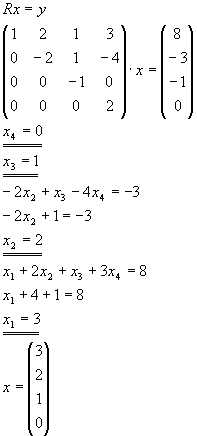
Aufgabe 13
Berechnen Sie die folgenden Determinanten
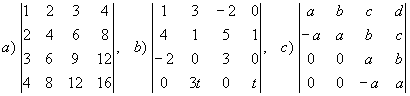
Lösung für Aufgabe 13
| a) |
Die Vektoren sind linear abhängig und es folgt
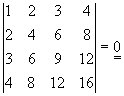
|
| b) |
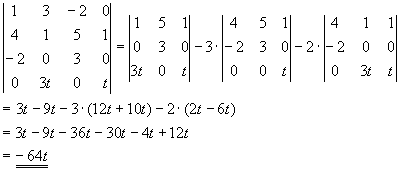
|
| c) |

|
Aufgabe 14
Die Zahlen 20604, 29716, 53227, 25755 und 78421 sind durch 17 teilbar. Zeigen Sie ohne explizite Berechnung
der Determinante, daß

ebenfalls durch 17 teilbar ist.
Lösung für Aufgabe 14
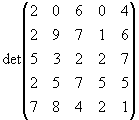
Jetzt wird die letzte Spalte erweitert.
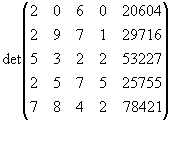
Die Spalte kommt wie folgt zustande:
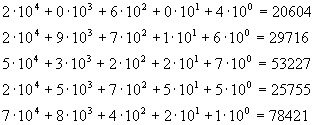
Die Determinante ändert sich nicht!
Jetzt wird aus der letzten Spalte die 17 herausgezogen
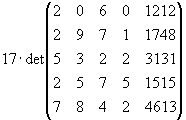
Aufgabe 15
| a) |
Die Darstellung des Vektors x bezüglich der kanonischen Basis lautet: (1,2,-1,3)T.
Wie lautet Sie bezüglich der Basis
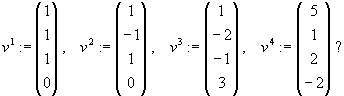
|
| b) |
Die Darstellung des Vektors z bezüglich der kanonischen Basis lautet: (1,2,3)T.
Wie lautet sie bezüglich der Basis
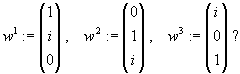
|
Lösung für Aufgabe 15
Aufgabe 16
| Zeigen Sie, daß für alle |
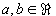 |
gilt |
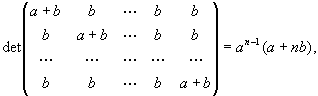
wobei n die Dimension der Matrix bezeichnet.
Lösung für Aufgabe 16
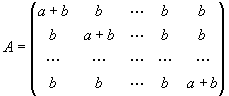
Mit A:=a·In, a:=(1,1,...,1)T und b:=(b,b,...,b)T
kann man die gegebene Matrix schreiben als A+abT.
Ist a=0, so ist die Matrix A+abT=abT singulär, und es gilt
det(A+abT)=0=an-1(a+nb).
Im Fall 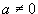 ist A regulär, und es folgt wegen
A-1=a-1In
ist A regulär, und es folgt wegen
A-1=a-1In
det(A+abT)=an(1+nba-1)=an-1(a+nb).
Aufgabe 17
Ermitteln Sie alle Nullstellen von det(A-tI) für
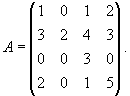
Lösung für Aufgabe 17
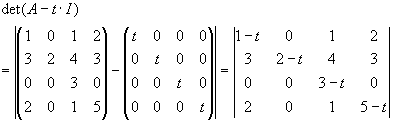
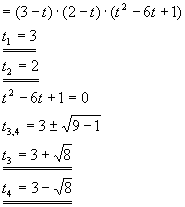
Aufgabe 18
| a) |
| Die lineare Abbildung |
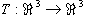 |
sei festgelegt durch |
T(e1)=3e3,
T(e2)=e1-e2-9e3,
T(e3)=2e2+7e3.
Geben Sie die Abbildungsmatrizen von T bezüglich der kanonischen Basis und der Basis
a1=(1,1,1)T,
a2=(1,2,3)T,
a3=(1,3,6)T an.
|
Lösung für Aufgabe 18
| a) |
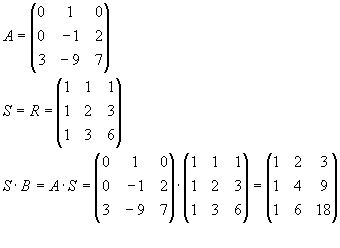
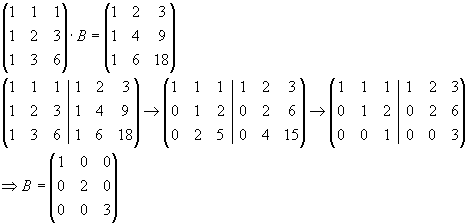
|
Aufgabe 19
W sei der von den Vektoren
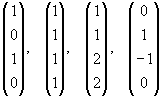
aufgespannte Teilraum des 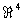 . Bestimmen Sie die Dimension von W, eine Basis von
W und mittels des Gram-Schmidt-Verfahrens eine Orthonormalbasis von W.
. Bestimmen Sie die Dimension von W, eine Basis von
W und mittels des Gram-Schmidt-Verfahrens eine Orthonormalbasis von W.
Wie lautet die Matrix der Orthogonalen Projektion des 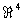 auf W und auf
auf W und auf
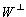 (bezüglich der kanonischen Basis)? Welchen Wert hat
(bezüglich der kanonischen Basis)? Welchen Wert hat
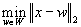
| für |
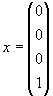 |
? |
Lösung für Aufgabe 19
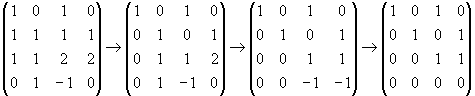
dim W = 3
Basis:
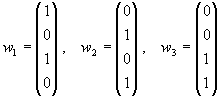
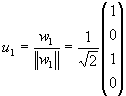
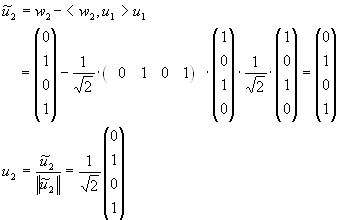
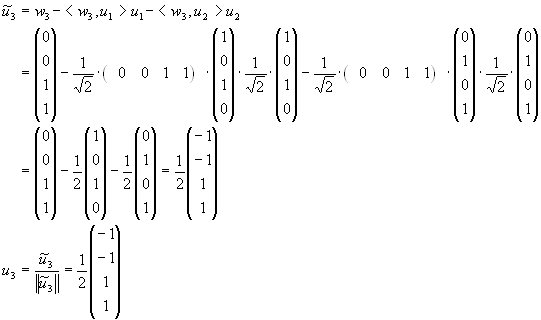
Orthonormalbasis:
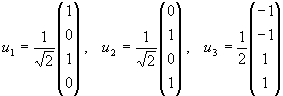
Orthogonale Projektion auf W:
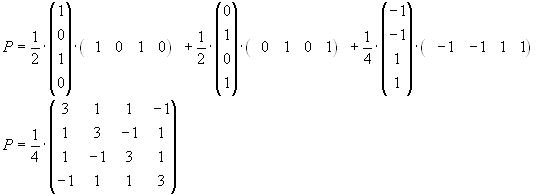
Orthogonale Projektion auf 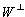 :
:
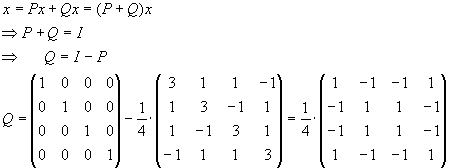
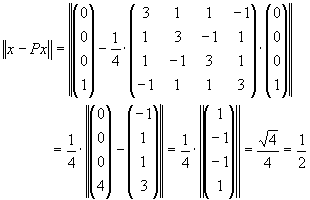
Aufgabe 20
| Es sei |
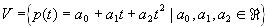 |
der Vektorraum der Polynome vom Grad 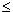 2 mit dem inneren Produkt 2 mit dem inneren Produkt |
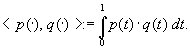
| i) |
Bestimmen Sie eine Basis des Unterraumes W orthogonal zu h(t)=2t+1.
|
| ii) |
Orthonormieren Sie mit dem Gram-Schmidt-Prozeß die Basis
v1(t)=1,
v2(t)=t,
v3(t)=t2
|
Lösung für Aufgabe 20
Aufgabe 21
| a) |
| Sei |
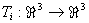 |
(i=1,2), |
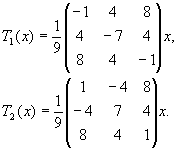
Untersuchen Sie, ob Ti eine Drehung oder eine Spiegelung beschreibt (i=1,2),
und bestimmen Sie ggf. Drehachse und Drehwinkel bzw. Spiegelungsebene.
|
| b) |
Bestimmen Sie die Matrix 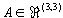 , die (bezüglich der kanonischen Basis
(e1, e2, e3)) die
45°-Drehung des , die (bezüglich der kanonischen Basis
(e1, e2, e3)) die
45°-Drehung des 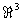 mit Drehachsenrichtung (1,1,0)T
beschreibt. mit Drehachsenrichtung (1,1,0)T
beschreibt.
Hinweis: Konstruieren Sie zunächst eine ONB (w1,
w2, w3) mit w1 parallel
zu (1,1,0)T, und stellen Sie die Abbildungsmatrix bezüglich dieser Basis auf.
|
Lösung für Aufgabe 21
Aufgabe 22
| Gegeben sei eine Matrix |
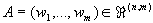 |
mit den Spaltenvektoren |
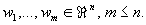
Lösung für Aufgabe 22
| a) |
Sei Rang A = m. Dann folgt aus ATAx=0 zunächst
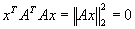 |
, |
d.h. Ax=0, und wegen der linearen Unabhängigkeit von
w1,...,wm erhählt man
x1 = ... = xm = 0.
Sei umgekehrt ATA regulär. Dann folgt aus Ax=0 zunächst
ATAx=0, und x=0 aus der Regularität von
ATA, d.h.
w1,...,wm sind linear unabhängig.
|
| b) |
Es sein Qx:=A(ATA)-1ATA=A.
Dann gilt
QA=A(ATA)-1ATA=A,
d.h. Qwj=wj, j=1,...,m, und daher Qx=x
für alle 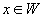 . .
Gilt 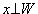 , so folgt (wj)Tx=0,
j=1,...,m, d.h. ATx=0, und daher , so folgt (wj)Tx=0,
j=1,...,m, d.h. ATx=0, und daher
Qx=A(ATA)-1ATx=0.
Aus diesen beiden Eigenschaften folgt für alle 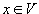
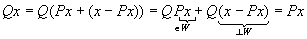 |
. |
|
| c) |
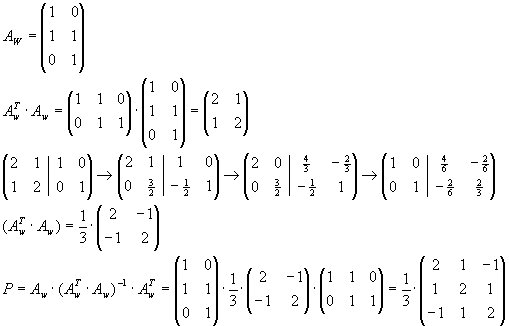
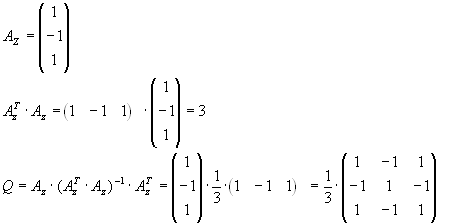
|
Aufgabe 23
| a) |
Für 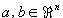 zeige man durch direkte Umformung der Determinante zeige man durch direkte Umformung der Determinante
det(In+abT) = 1 + aTb.
|
| b) |
Man leite hieraus
det(A + abT) = detA·(1 + bTA-1a)
für reguläre Matrizen 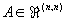 und und 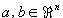 her. her.
|
| c) |
Welcher Wert ergibt sich für die Determinante einer Householder-Matrix? |
Lösung für Aufgabe 23
| a) |
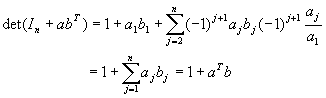 |
| b) |
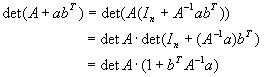 |
| c) |
det(I+2wwT)=-1 |
Aufgabe 24
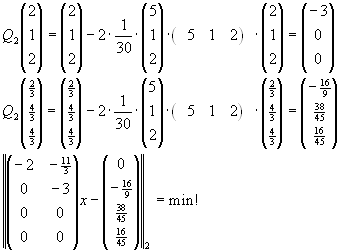
Lösen Sie das lineare Ausgleichsproblem
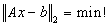
für
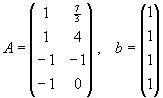
unter Benutzung
| a) |
von Householder-Transformationen (QR-Zerlegung), |
| b) |
der Normalgleichungen. |
Lösung für Aufgabe 24

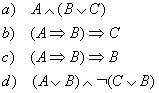

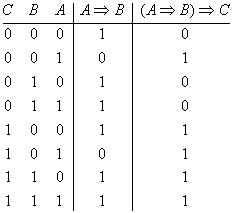
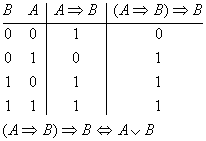

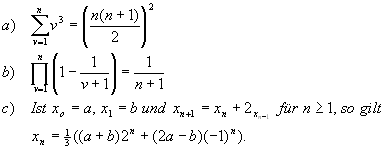
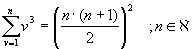
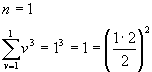
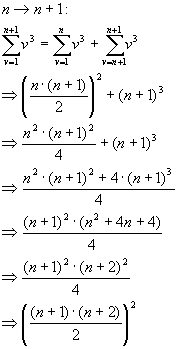
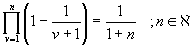
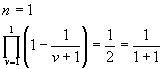
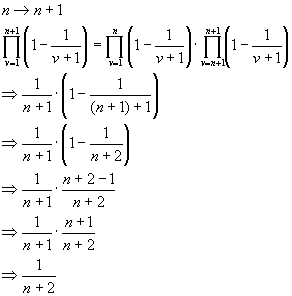
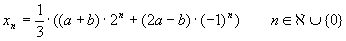
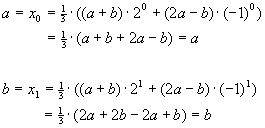
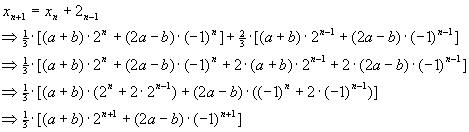
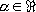 sind die folgenden Vektoren linear abhängig?
sind die folgenden Vektoren linear abhängig?
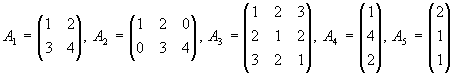 .
.
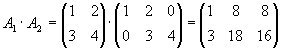
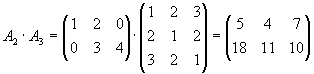
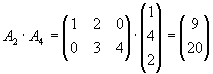
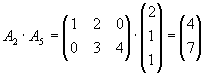
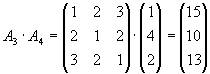
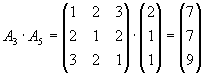
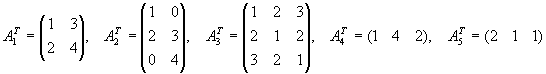
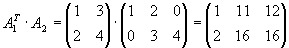
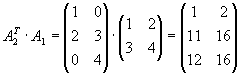
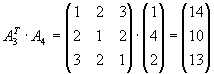
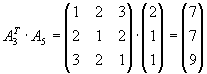
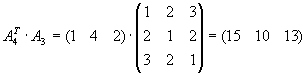
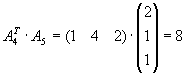
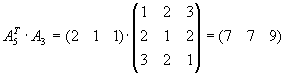
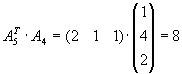
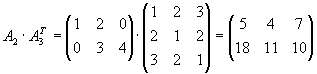
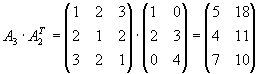
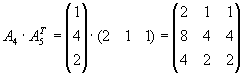
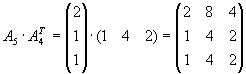
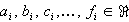
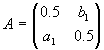
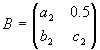
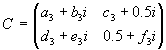
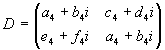
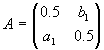
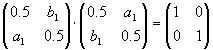
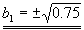
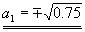
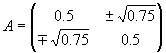
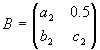
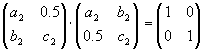
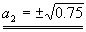
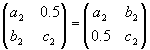
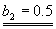
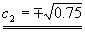
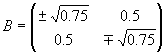
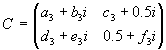
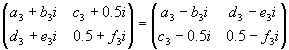
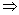
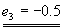
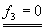
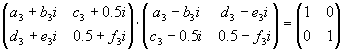
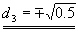
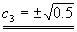
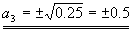
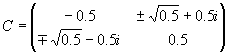
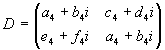
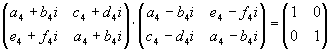
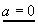
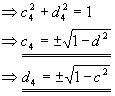
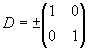
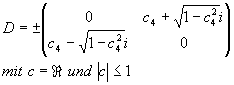
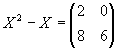
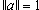 . Daraus werde die
(n, n)-Mtrix A = In - 2 a aT (A ist eine sog.
Householder-Matrix) gebildet. Man berechne A2. Was folgt hieraus für A-1
und allgemein für AP (p ganz)?
. Daraus werde die
(n, n)-Mtrix A = In - 2 a aT (A ist eine sog.
Householder-Matrix) gebildet. Man berechne A2. Was folgt hieraus für A-1
und allgemein für AP (p ganz)?
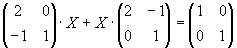
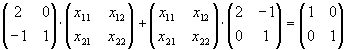
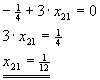
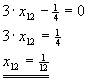
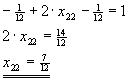
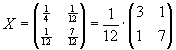
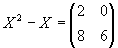
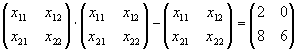
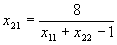
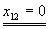
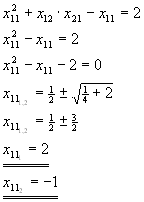
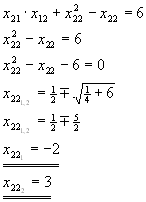
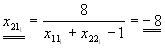
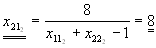
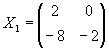
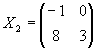
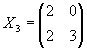
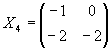
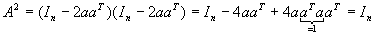
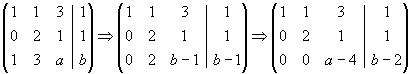
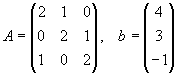
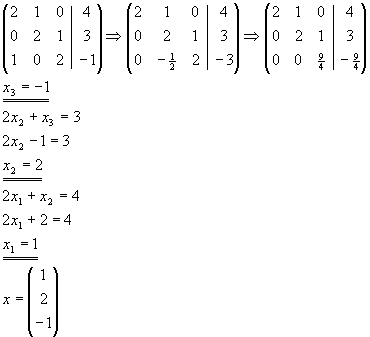
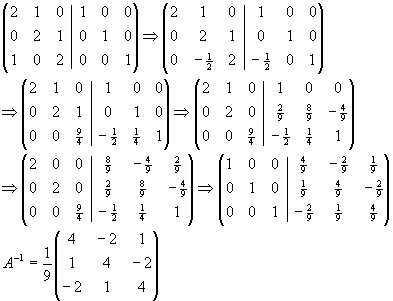
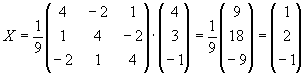
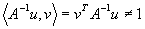
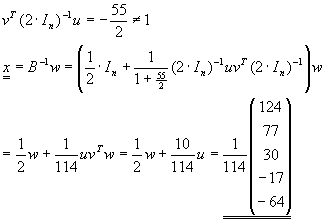

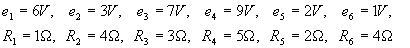
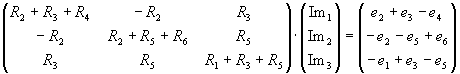
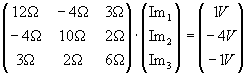
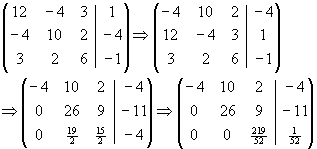
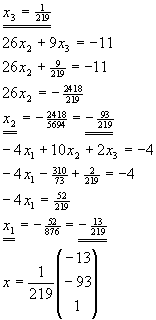
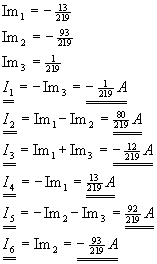
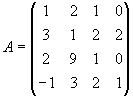
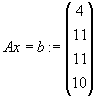
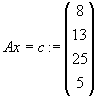

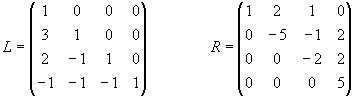
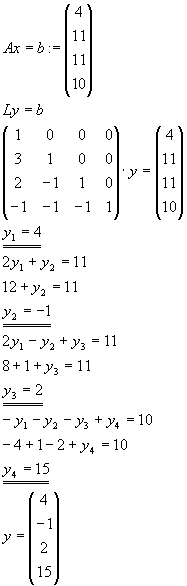
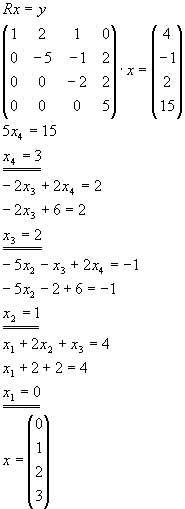
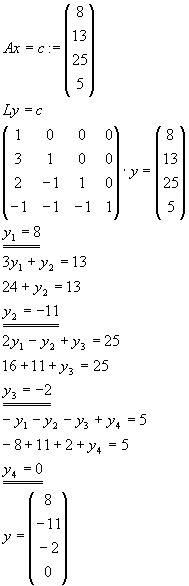
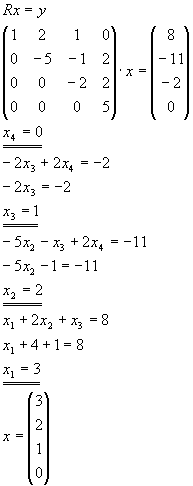
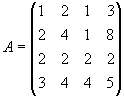
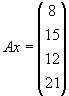
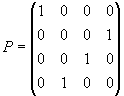
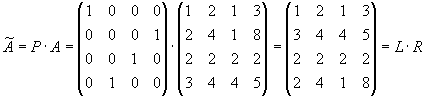
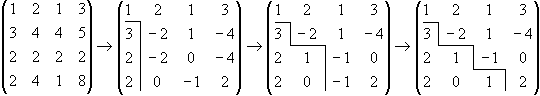
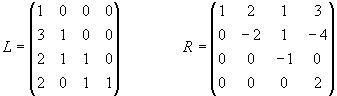
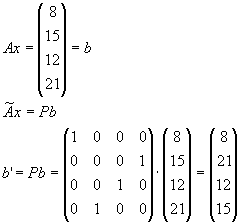
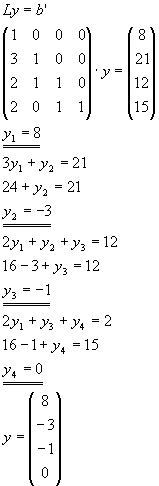
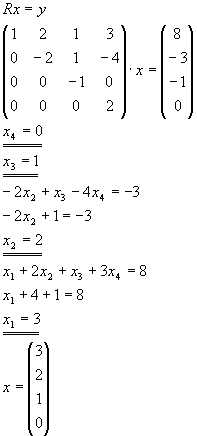
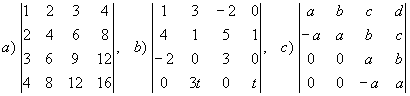
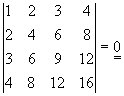
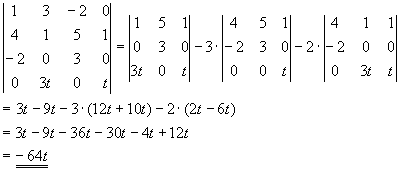


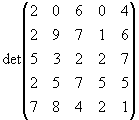
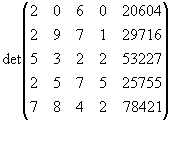
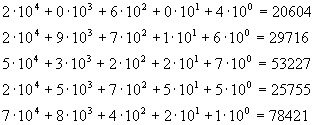
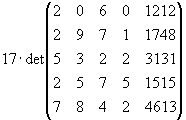
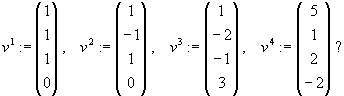
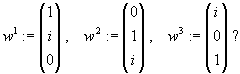
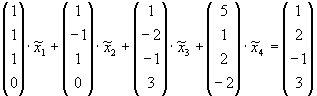
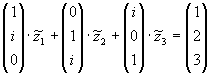
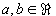
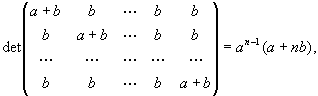
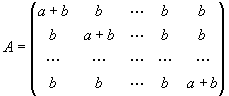
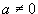 ist A regulär, und es folgt wegen
A-1=a-1In
ist A regulär, und es folgt wegen
A-1=a-1In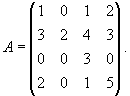
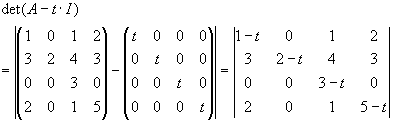
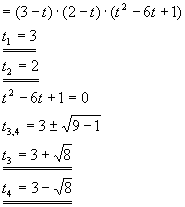
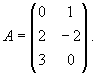
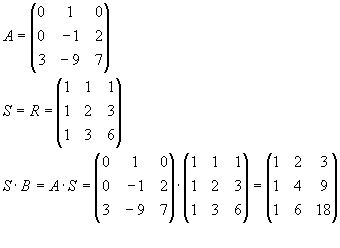
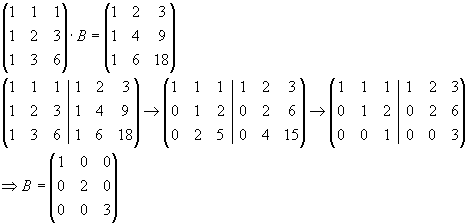
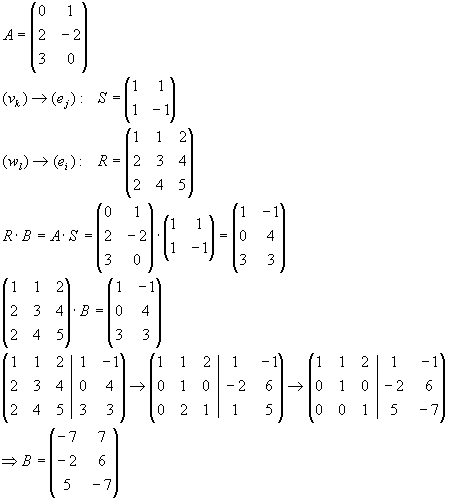

 . Bestimmen Sie die Dimension von W, eine Basis von
W und mittels des Gram-Schmidt-Verfahrens eine Orthonormalbasis von W.
. Bestimmen Sie die Dimension von W, eine Basis von
W und mittels des Gram-Schmidt-Verfahrens eine Orthonormalbasis von W.
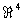 auf W und auf
auf W und auf
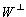 (bezüglich der kanonischen Basis)? Welchen Wert hat
(bezüglich der kanonischen Basis)? Welchen Wert hat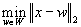
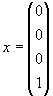
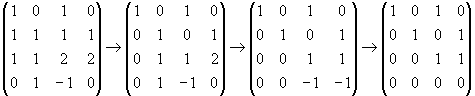
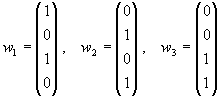
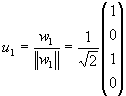
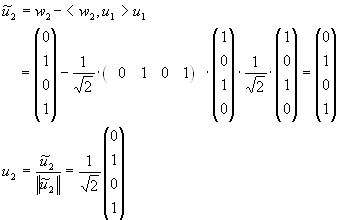
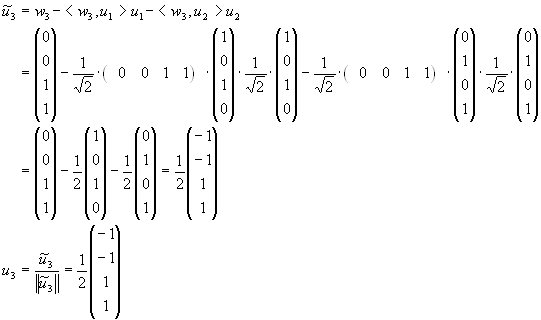
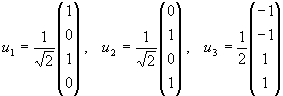
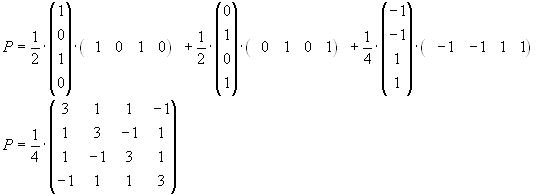
 :
: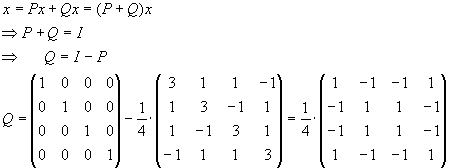

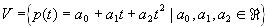
 2 mit dem inneren Produkt
2 mit dem inneren Produkt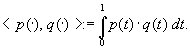
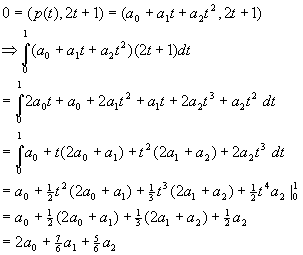
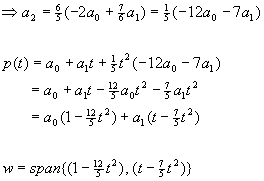
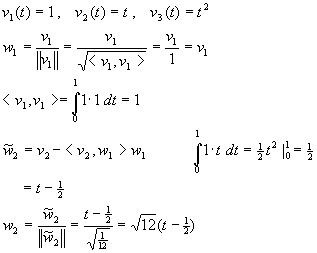
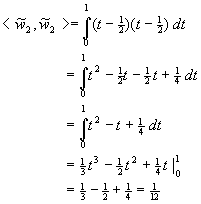
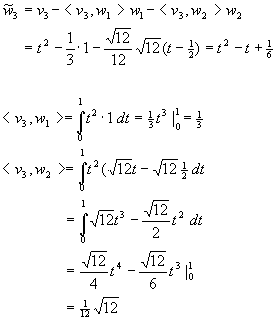
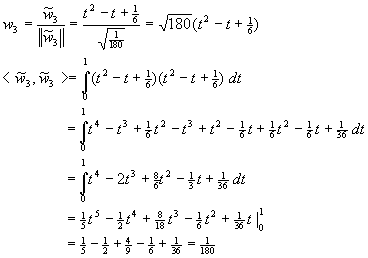
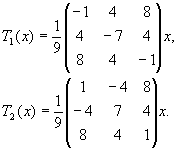
 , die (bezüglich der kanonischen Basis
(e1, e2, e3)) die
45°-Drehung des
, die (bezüglich der kanonischen Basis
(e1, e2, e3)) die
45°-Drehung des 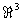 mit Drehachsenrichtung (1,1,0)T
beschreibt.
mit Drehachsenrichtung (1,1,0)T
beschreibt.
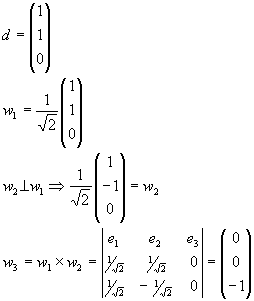
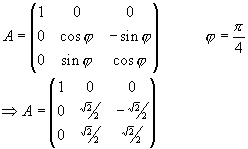
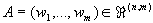
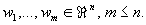
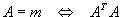 regulär.
regulär.
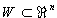 , so besitzt die orthogonale Projektion des
, so besitzt die orthogonale Projektion des 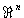 auf W die
Matrixdarstellung
auf W die
Matrixdarstellung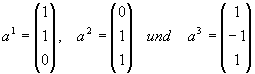
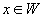 .
.
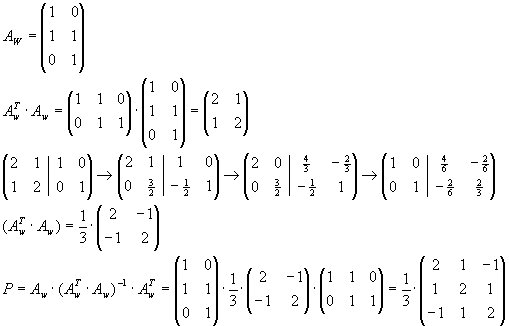
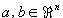 zeige man durch direkte Umformung der Determinante
zeige man durch direkte Umformung der Determinante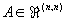 und
und 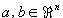 her.
her.